An Intuitive way to see Priors
An intuitive illustration of a prior from McElreath’s Statistical Rethinking.
Bayesian inference is really just counting operation over all possibilities that events can branch out to. In order to make good inference about what actually happened, it helps to consider everything that could have happened and weigh each one against the other. A Bayesian analysis is a garden of forking data, in which alternative sequences of events are cultivated.

As we learn about what did happen, some of these alternative sequences are pruned or become statisitcally insignificant. In the end, what remains is only what is logically consistent with our knowledge.
Counting
We can think of probability operations as counting operations i.e each multiplication or addition of any distribution or function essentially is a way to recount the happenings of certain events.
Suppose there’s a bag, and it contains four marbles. These marbles come in two colors: blue and white. We know there are four total marbles in the bag, but we don’t know how many are of each color.
I will denote blue marbles as B and white as W. Say we draw 3 balls randomly for the bag.
If we want the probability of observing a BWB from any one of the options we make a tree diagram of the possibilities and count the ways our desired outcome is possible. The more ways an option has, the higher its probability. We can do so for each option and see which has the highest chance. Another way of saying this is that suppose A and B can both individually cause C. Then if A causes C in many more ways than B, observing C makes A more plausible than B.
The way to count for Option 2 from above would be 1 * 3 * 1 = 3 ways.
Likewise Option 3 would have : 2 * 2 * 2 = 8 ways
 Counts for BWB
Counts for BWB
Convince yourself that for the observation of BWBB, the counts would be as follows. We will continue with this example.
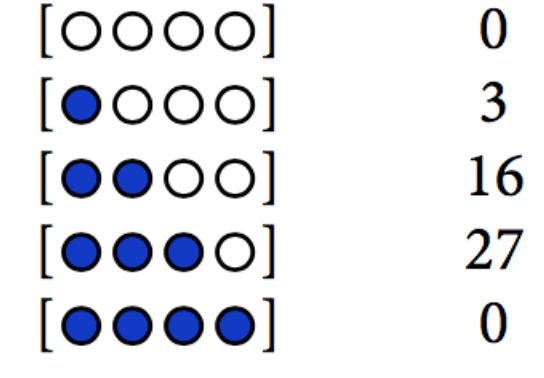 Counts for BWBB
Counts for BWBB
Prior
So for each option, the more number of ways it makes the data observed possible, the higher its chance of being the true option. So now option 3 is clearly the most likley. (you may observe that option 2 and 3 were very close in BWB but become quite different in BWBB! Why would this happen? )
Now suppose we had picked our bag from another ‘meta-bag’. And say in this meta-bag there are different number of bags belonging to each option. Say there were two option 2 bags. So now the total number of ways option 2 would be the source of BWBB would be 2 into 16. We do this for each bag to get an updated number of ways each option makes the data possible. The number in our ‘meta-bag’ is given as Factory Counts below.
 'Meta-bag'-ness
'Meta-bag'-ness
So now we see the Option 3 has surpassed 4 as there are more ways it could be the source. So we would say Option 3 is most likely. The number of each in the ‘meta-bag’ altered the number of ways something could happen due to an option by making the option more or less prevelant that the others. This is what is called as a prior. In this case it happened to be a hardened fact but a belief would act in the same way. A belief based on good judgment estimates the the frequence of a option in a sea of options before an observation is made. That is why it is critial for beliefs/priors to be made before or be independant of any observation.
